Research Highlights

Topological states of matter exhibit fascinating phenomena, such as quantised transport and remarkably robust physical properties. While topology was first introduced to understand the quantum behaviour of electrons in solids, topological states can now be engineered in many different platforms including photonics, ultracold atomic gases and classical mechanics. Our research focuses on how we can exploit the features of these different systems to predict new phenomena and to deepen our understanding of topological physics.

To find out more, scroll down for our research highlights or check out our recent review articles:

Topological Physics in Higher Spatial Dimensions

Dimensionality plays a key role in how we understand topological physics, as different topological states can exist in systems with different numbers of spatial dimensions. We have been particularly interested in what new phenomena can arise in hypothetical systems with more than the usual three spatial dimensions. Although this may seem abstract, recent developments in ultracold atoms and photonics have opened the door to exploring such higher-dimensional topological physics experimentally, using techniques such as “synthetic dimensions” and “topological pumping”. We have proposed how these techniques can be developed and applied, and collaborated on an experiment to probe the first signatures of a 4D topological effect in the laboratory.

Recent publications about topological physics in higher dimensions are below:

Probing Topological & Geometrical Properties

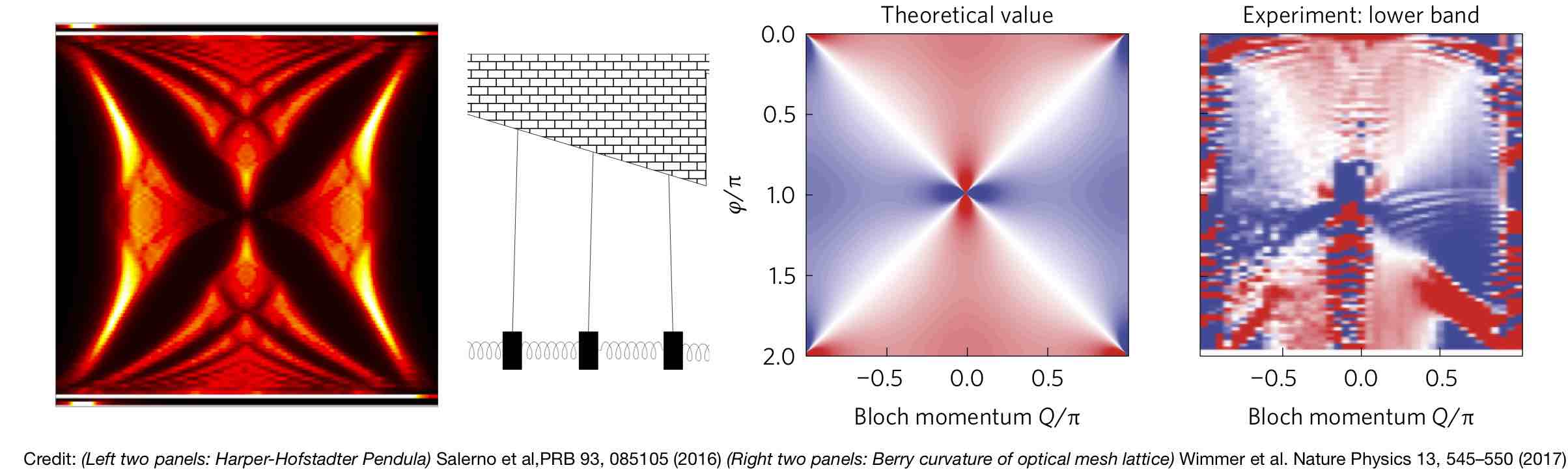
Exploring topological physics across different platforms requires the development of different techniques for designing and probing the topological and geometrical properties of a system. We have proposed new approaches to engineer topological lattice models in photonics, cold atoms and classical mechanical set-ups. We have also studied how key characteristics of the resulting energy bands, such as the geometrical Berry curvature, can be measured in experiments.

Recent publications about designing and measuring geometrical and topological properties are below:

Momentum-Space Magnetism

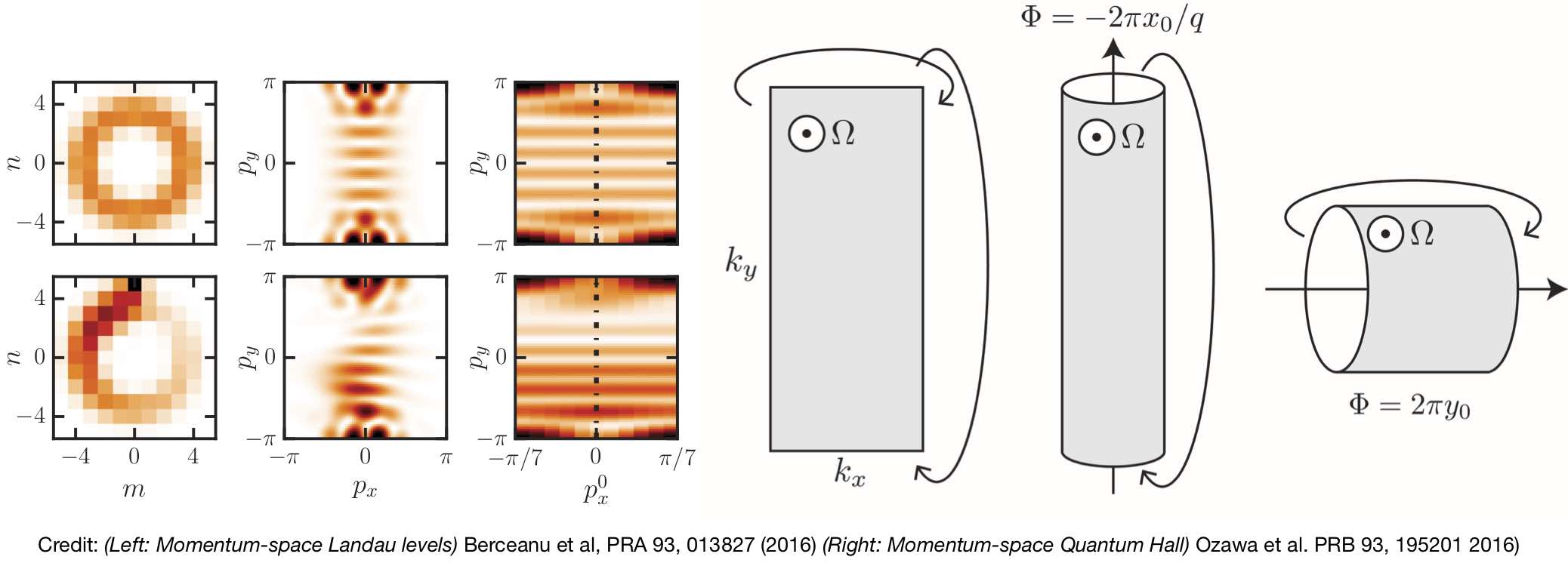
The Berry curvature is a geometrical property of an energy band that is closely related to key topological invariants of the band. A powerful way to understand the geometrical Berry curvature is to realise that it acts like a magnetic field, except in momentum space. Inspired by this analogy, we have explored the physics of systems with Berry curvature, showing that current experiments with photons or cold atoms could be extended to reveal momentum-space analogues of many familiar phenomena, including Landau levels, magnetic lattice models and even the quantum Hall effect.

Recent publications about momentum-space magnetism are below: